- Introduction
- What Are Dragon Curves?
- Creating Dragon Curves
- Dragon Curve in Turtle Graphics
- Further Reading and Exploration
- References
Introduction
This article is about Dragon curves. Before diving into the subject I want to say a few words about how this article came about.
When I first built my own turtle programming environment, one of the first programs I wrote was to draw a dragon curve. I'm not sure how I got to know about them, it's been years.
As I've written elsewhere I rewrote my turtle programming environment called Picoturtle in C++ and Lua [1]. And then I've migrated the older programs in the previous version into the newer Lua syntax. I was trying to organize all the curves related programs into one where I encountered my dragon curve program again. This time I wanted to enhance the program to built more variants and I was hoping to study them in more detail. I'm writing this article as I'm exploring Dragon Curves anew.
What Are Dragon Curves?
Dragon curves are an interesting family of fractal curves which can be generated by simple recursive algorithms or methods. They were discovered by a bunch of physicists in the 1960s. You can read more about their history at the wikipedia page [2]. They are called dragon curves because at higher orders the curve starts to look more and more like an abstract picture of the Chinese dragon.
Interesting Properties of Dragon Curves
Lorem ipsum, dolor sit amet consectetur adipisicing elit. Dolorum harum qui quidem optio vitae atque perferendis explicabo veritatis, error fugiat, eveniet voluptatibus? Dignissimos ad deleniti consectetur nostrum ducimus expedita fugiat!Creating Dragon Curves
Let's take a look at how we can make dragon curves. Since the method to create a dragon curve is recursive therefore while making the curve by hand we must repeat the same process each time but with the previous order curve. While writing a program to create the dragon curve we write a simple recursive procedure.
Paper Dragon Curves
 To create a simple dragon curve by hand, take a strip of paper, say
10 inches long and 1 inch wide. We can call this strip of paper, without
any curves or folds a "Dragon Curve of order 0".
To create a simple dragon curve by hand, take a strip of paper, say
10 inches long and 1 inch wide. We can call this strip of paper, without
any curves or folds a "Dragon Curve of order 0".
 Now take the strip of paper and fold it width-wise at the center of
the long side. You should get a folder piece half as long as the
original and the same width. If you started with 10in X 1in paper,
then you should now have one with 5in X 1in size.
This folded piece of paper when unfolded such that the fold is
open 90 degrees (or at a right angle) is a "Dragon curve of order 1".
Remember when unfolding higher order curves that each fold is to
be opened only at 90 degrees whether it is a valley or mountain fold.
Now take the strip of paper and fold it width-wise at the center of
the long side. You should get a folder piece half as long as the
original and the same width. If you started with 10in X 1in paper,
then you should now have one with 5in X 1in size.
This folded piece of paper when unfolded such that the fold is
open 90 degrees (or at a right angle) is a "Dragon curve of order 1".
Remember when unfolding higher order curves that each fold is to
be opened only at 90 degrees whether it is a valley or mountain fold.
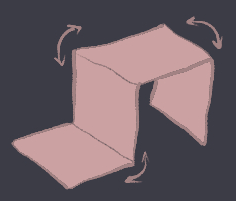 To get the next order of dragon curve from the previous - take the
curve of the previous order, and without unfolding, fold it again
at the same side as the previous fold. So if the first fold was
a valley fold, then next fold should be valley fold too. Now when
you unfold the paper you get a dragon curve of order 1 greater than
the previous fold.
If you started with 10in X 1in paper, then order #2 will have
dimensions 2.5in X 1in and order #3 will have dimensions
1.25in X 1in.
To get the next order of dragon curve from the previous - take the
curve of the previous order, and without unfolding, fold it again
at the same side as the previous fold. So if the first fold was
a valley fold, then next fold should be valley fold too. Now when
you unfold the paper you get a dragon curve of order 1 greater than
the previous fold.
If you started with 10in X 1in paper, then order #2 will have
dimensions 2.5in X 1in and order #3 will have dimensions
1.25in X 1in.
Mathematical Interpretations
The maths behind the dragon curve is really simple. Firstly, the maths is not worried about the structure or dimensions of the curve at all. At its most abstract the dragon curve is a sequence of folds. And there are only two kinds of folds:
- Mountain fold (M): Where the fold lies above the nearby paper. Imagine a fold shaped like an inverted V like '/\'.
- Valley fold (V): Where the fold below above the nearby paper. Imagine a fold shaped like a 'V'.
The dragon curve being a sequence of these folds, we can write a dragon curve in shortened form like this...
- Order 0: Empty sequence
- Order 1: V
- Order 2: V V M
- Order 3: V V M V V M M
- Order 3: V V M V V M M V V V M M V M M
Length of the Dragon Curve String
Let's take the paper folding analogy and try to understand the dragon curve's length. When there are already folds in a piece of paper, and we fold it once more then we are roughly doubling the number of folds. In fact we notice that the number of folds is a function of the order. Let's say that is the dragon curve function for order N. And represents the length of the dragon curve string. Then we have the following equation to get the value of the length.
We can also write this in the recursive form here.
L-system interpretation of Dragon Curve
Lindenmeyer-system or L-system is a string rewriting system which was develped by a biologist in the 1960s while studying the growth structures of plants - and wheter they could be modeled using recursive methods.
An L-system consists of an alphabet and two sets of rules. The alphabet defines characters which can be present in the string. The first set of rules defines rules of production for each iteration i.e. what replaces each character in the next iteration. The second set of rules defines a graphical interpretation of each character so that a pictorial view of the current string can be created.
In the L-system interpretation of Dragon Curve the alphabet of the system is such that a set of alphabets defines the Valley fold and another set of alphabets defines a Dragon fold. This helps in an easier interpretaion rules for turtle graphics instructions.
1. Characters for Dragon Curve & Drawing Rules
- F (variable): draw forward
- G (variable): draw forward
- + (constant): turn right 90 degrees
- - (constant): turn left 90 degrees
Note: in an l-system variables have rewriting rules, constants don't i.e. they don't change across iterations.
The string "F+G" defines a mountain fold and "F-G" defines a valley fold.2. Rewriting Rules
- F -> F+G
- G -> F-G
Creating Dragon Curves in 3D
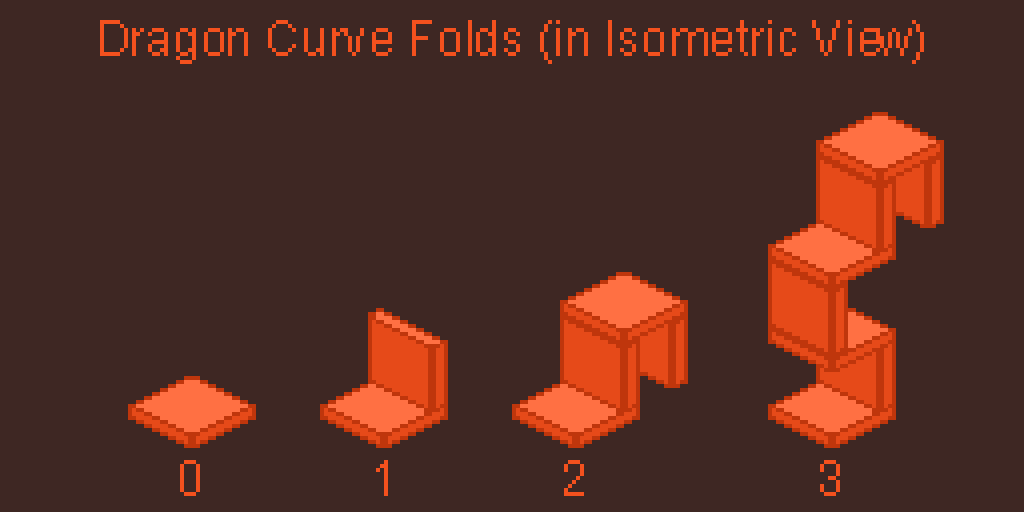
One can construct Dragon Curves in a 3-dimensional by applying the same principles described in the paper folding section. We start with a flattened block and its upright variant. Now we can stack them on top/below each other to create the required fold structures.
The next figure illustrates the folds of the first four orders in 3D isometric view. You can see that at order 3 we can already see some interesting shape emerge. NOTE: this illustration is different from the procedure described above in one important aspect. I've shown the higher order curves by adding more paper so as to better visualize it.
Dragon Curve in Turtle Graphics
Introduction to PicoTurtle Graphics
PicoTurtle is a simple Lua Turtle Graphics program that I built sometime ago. It has its own desktop app where one can explore a graphics program using a lua editor, turtle canvas and lua console views. You can find out more about picoturtle at it webpage [1].
L-System Dragon Curve using Turtle Graphics
In this section I show a program which defines a dragon curve using L-system rules. The L-system interpreter is a simple program I built myself. Once the rules are defined, the l-system is allowed to interpret the axiom with the rules for a given number of iterations. The drawing rules specify how the string generated by the l-system is interpreted on the canvas. The result is a drawing of the dragon curve on the turtle canvas.
The next two listings are first the Lua program to define and draw the Dragon curve, followed by the image snapshot of the resulting turtle canvas. There are comments in the Lua code which explain each step in the program.
--- dragon_curve_lsystem.lua: draw a dragon curve using an
-- l-system string rewriting system.
--
-- author: Abhishek Mishra
-- date: 25/03/2023
-- imports
local t = t or require 'picoturtle'.new()
local lsystem = require 'lsystem'
local co_eval_lsystem = lsystem.co_eval_lsystem
-- rules for rewriting dragon curve string
-- note that '+' is written as 'P'
-- and '-' is written as 'M'
local dragoncurve_rules = {
F = 'FPG',
G = 'FMG'
}
-- turtle drawing rules for each character in
-- the dragon curve l-system alphabet
local dragoncurve_turtle_rules = {
F = function () t:fd(5) end, -- draw forward
G = function () t:fd(5) end, -- draw forward
P = function () t:right(90) end, -- turn right 90 degrees
M = function () t:left(90) end, -- turn left 90 degrees
}
-- starting string a.k.a axiom
local axiom = 'F'
-- number of iterations of string rewriting to run
local num_iter = 14
-- local vars to setup the lsystem interpreter
local avail = true
local eval_lsystem = co_eval_lsystem()
-- store the last string to draw
local last_string = axiom
-- start the l-system co-routine for the given num_iter iterations,
-- axion, and the rewriting rules.
while avail do
avail, axiom = coroutine.resume(eval_lsystem, axiom, dragoncurve_rules, num_iter)
if avail then
if axiom ~= nil then
last_string = tostring(axiom)
end
end
end
-- setup the turtle settings
local cw, ch = t:canvas_size(1024, 1024)
t:clear(40, 40, 60)
t:penwidth(2)
t:pencolor('blue')
t:penup()
t:setpos(350, ch - 250)
t:pendown()
t:heading(180)
-- draw the last string using the turtle rules
command_interpreter(last_string, dragoncurve_turtle_rules)
-- take a snapshot of the turtle canvas
t:snap('out/dragon_curve_lsystem.png')

Dragon Curve Recursive Program
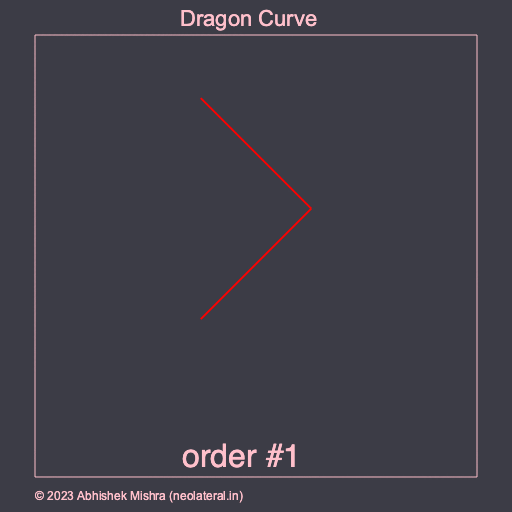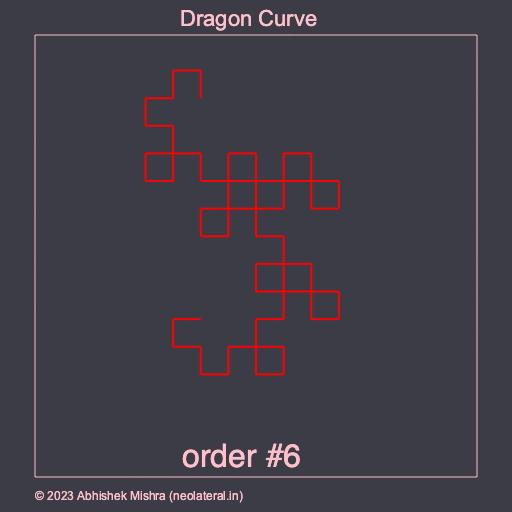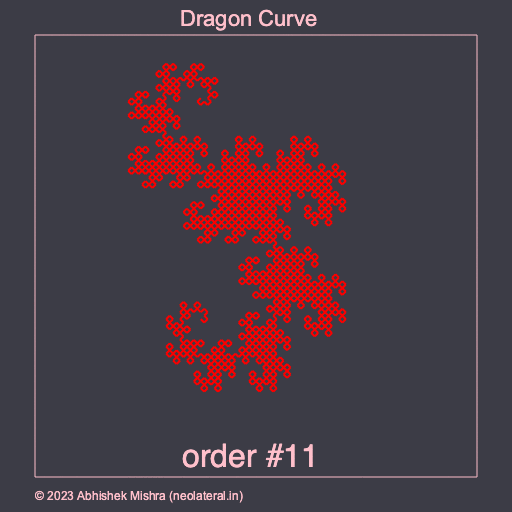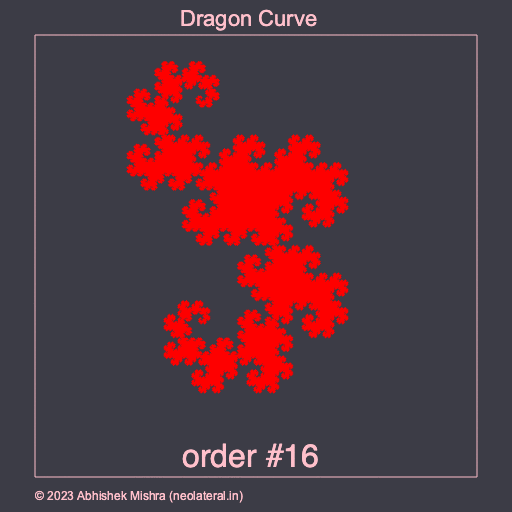
This section presents a Dragon Curve implementation using a simple recursive program, without using an L-system interpreter. One can see the recursive nature of the Dragon Curve perhaps more clearly here.
First the contents of dragon_curve.lua are presented, which contains a Lua module with a single function to draw a Dragon Curve using turtle graphics. Next we provide outputs of two programs as images (one a PNG another a GIF) which were generated using this module.
--- dragon_curve.lua: Recursive implementation of the Dragon curve in turtle graphics.
--
-- author: Abhishek Mishra
-- date: 22/03/2023
-- constant used to recurse downwards
local SQRT_OF_HALF = (1 / 2) ^ (1 / 2)
--- main dragon curve drawing function
-- accepts the length and order of the curve
-- as well as a turtle reference to draw with
function dragonCurve(turtle, order, length)
turtle:right(order * 45)
dragonCurveRecursive(turtle, order, length, 1)
end
--- inner recursive function which turns right
-- or left based on the sign, and then calls the
-- lower order curve function
function dragonCurveRecursive(turtle, order, length, sign)
if order == 0 then
-- if order is 0, just move forward and return
turtle:forward(length)
else
-- if order is not 0, draw lower order curve
-- with sign 1 and length scaled by sqrt(1/2)
-- then turn right
-- and then draw lower order curve with sign -1
-- and length scaled by sqrt(1/2)
dragonCurveRecursive(turtle, order - 1, length * SQRT_OF_HALF, 1)
turtle:right(sign * -90)
dragonCurveRecursive(turtle, order - 1, length * SQRT_OF_HALF, -1)
end
end
local dg = {}
dg.dragonCurve = dragonCurve
return dg
Further Reading and Exploration
Donald Knuth and Dragon Curves
Here's an interesting video about Donald Knuth's experience about a Dragon Curve wall art at his home.