Recursive Subdivision Of Curves
The Algorithm in 1-D
- Building and Running the Program
The fBm Curve
Displaying the Curve
main.lua
conf.lua

Version	Date	Comments
0.1	25/11/2024	Initial version

Recursive Subdivision Of Curves

This is a literate program (written in litpd ¹) that demonstrates creating fractal paths/curves starting with a simple curve with a few line segments. The algorithm is from the classic paper on the topic of such methods ². The paper discusses the use of recursive subdivision methods to create fractal curves and surfaces. This method and its variations have been frequently used as they produce decent results and the 1-D version that we use here has linear complexity.

This article is divided into two sections:

Algorithm: We discuss the recursive subdivision algoritm and its properties in this section.
Program: We develop a love2d simulation to demonstrate the use of this algorithm in various scenarios and with varying parameters.

Here is a youtube video which shows the simulation in action:

The Algorithm in 1-D

The paper mentioned in the introduction ³ describes the algorithm we are about to discuss as "... a recursive algorithm for generating approximations to the sample paths of one dimensional fBm" (fBm stands for fractional Brownian motion). Thus the algorithm generates in every run a sample Brownian motion path between the input end-points.

Since this algorithm is recursive in nature it can be repeated to any level of detail. The detail in the curve increases with the recursive depth of the program. This recursive depth should be used to produce a curve that retains sufficient detail at the highest zoom level used in the graphical application.

Now, let's jump into the algorithm. In the original paper the algorithm is written in Pascal, however here I present it informally as we will later develop the program in lua.

Step 1: End-points of the Curve: First we must established the start and end-point of the curve. These will serve as the starting input to the recursive subdivision. These points on 1-d are simple real values which can be given as user input or assigned to random values.
Step 2: Establish the number of points: The paper provides states that for detail level N, the number of points in the curve should be 2^N. The maxlevel N can be a user input.
Step 3: Recursive Subdivision: In the third step we take a segment and find its midpoint. Then we perturb the midpoint by a random amount. This gives us two new segments. We run the process till the segments are of zero lengths and cannot be subdivided. Each recursive step doubles the number of segments to be processed in the next round. The entire process is started with the first and last points decided in the Step 1.

The amound of perturbation at each level of recursion decreases as we subdivide smaller and smaller segments. The amount of randomness added is the Hurst Exponent - which is related to the shape of the fBm. The value of the Hurst Exponent decides the roughness/smoothness of the generated curve.

Building and Running the Program

See the Makefile in the current directory to see how to build and run the program.

The fBm Curve

The fbmcurve.lua file defines the FBMCurve class. It represents a single curve defined using recursive subdivision. The class is defined using the middleclass library.

id: fbmdeclaration

local Class = require "middleclass"

local FBMCurve = Class("FBMCurve")

Constructor

The class constructor accepts four optional arguments seed, num_levels, max_height, and h.
The seed argument is an input to the random number generator. The random number generator is used to create the perturbation in the midpoint when subdividing a line segment. The default value of seed is 1.
The num_levels argument controls how many points will be generated in the curve. It represents the amount of detail required in the curve. The higher the value, the greater the number of points in the curve. The default value for num_levels is 9.
The max_height is the maximum value of the curve generated. It is used to generate the first and last points of the curve. The x-values of each point in the curve is the index in the sequence of points.
h is a parameter which controls roughness/smoothness of the generated curve. It's default is 0.01.
The constructor uses the inputs to initialize some state for the curve.
The number of points num_points in the curve is first set equal to 2^num_levels + 1.
A new table points is created to store the points of the curve.
The first and last points of the curve are created using the random number generator.
A default initial value is assinged to all the other points of the curve.
The h value refers to the Hurst Exponent and is used to calculate the ratio of dampening of the perturbation at each recursive depth. The dampening increases as we descend into sub-dividing smaller and smaller line segments. The value of h affects the roughness/smoothness of the generated curve.
The ratio of dampening is defined as 2^-h.

id: fbmconstructor

--- Create a new FBMCurve object
-- @param seed (number) The seed for the random number generator (default 1)
-- @param num_levels (number) The number of levels of the curve (default 9)
-- @param max_height (number) The max value of y-axis (default window height)
-- @prama h (number) Hurst Expoonent (default 0.01)
function FBMCurve:initialize(seed, num_levels, max_height, h)
    self.seed = seed or 1
    self.num_levels = num_levels or 9
    self.max_height = max_height or love.graphics.getHeight()
    self.h = 0.01

    self:generate()
end

Gaussian Random Number Generator

The gauss function is a utility function to generate random numbers using the inbuilt pseudo-random generator with a mean of 0 and a standard deviation of 1.
The seed of the random generator is based on the input index and the seed provided by user input. This allows us to create random number sequences which can be replicated if the same input is provided again.
The function is used in the subdivision process.

id: fbmgauss

-- Generate a Gaussian (normal) distributed random number
function FBMCurve:gauss(index)
    -- Seed the RNG uniquely for deterministic results
    local combined_seed = self.seed + index
    math.randomseed(combined_seed)

    -- Generate two uniform random numbers (0, 1)
    local u1 = math.random()
    local u2 = math.random()

    -- Box-Muller transform
    local z0 = math.sqrt(-2.0 * math.log(u1)) * math.cos(2.0 * math.pi * u2)

    -- Return a Gaussian random number with mean 0 and standard deviation 1
    return z0 
end

Subdivision Implemenation

In the subdivision implementation we define two methods viz. generate and subdivide.
The generate method sets up the parameters for the subdivision using the user provided input. The length of the curve is decided, the array of points are created to match the length, and the first and last points are assigned random y-values based on the maximum y-value of the display. The other values in the array are given initial values which are later changed by the subdivide method.
Lastly, the generate method calls the subdivide method with the first and last counts of the points array, and a measure of standard division which is based on the input Hurst Expoonent.
The subdivide method is a recursive function to create a new midpoint for the given range, until we are down to a range with width 1.
Each midpoint is the mean of the left and right values of the range added to a random value generated using the gauss function defined earlier multiplied with the given standard deviation. (Note the standard deviation of the value returned from gauss is 1). The scaling of the random adjustment reduces with the depth of recursion.

id: fbmsubdivision

function FBMCurve:generate()
    -- use the seed to create a new random number generator
    math.randomseed(self.seed)

    -- the number of points is a function of num_levels
    self.num_points = (2 ^ self.num_levels) + 1
    -- initialize the points array
    self.points = {}

    -- random start and end points using the given seed
    -- in the range [0, num_levels]
    self.points[1] = love.math.random(1, self.max_height)
    self.points[self.num_points] = love.math.random(1, self.max_height)

    -- fill the rest of the points with 0
    for i = 2, self.num_points - 1, 1 do
        self.points[i] = 10
    end

    -- the ratio of the perturbation is a function of the Hurst Exponent
    self.ratio = 2 ^ (-self.h)

    -- define the standard deviation
    local std = self.ratio * self.num_levels

    -- start with the subdivision of the outermost segment
    self:subdivide(1, self.num_points, std)
end

function FBMCurve:subdivide(left, right, std)
    -- get the midpoint of the segment
    local mid = math.floor((left + right) / 2)

    -- only proceed if the midpoint is distinct from the left and right
    if mid ~= left and mid ~= right then
        -- the y-value at the midpoint is the mean of the left and right points
        -- with an additional random compnent multiplied with the standard
        -- deviation
        self.points[mid] = (self.points[left] + self.points[right]) / 2.0 + self:gauss(mid) * std

        -- define the standard deviation for the next level of recursion,
        -- by multiplying with self.ratio
        local stdmid = std * self.ratio

        -- subdivide the left and right segments
        self:subdivide(left, mid, stdmid)
        self:subdivide(mid, right, stdmid)
    end
end

Class definition

In this section we bring all the parts of the FBMCurve class together, and generate the program.

file: fbmcurve.lua

@<fbmdeclaration@>

@<fbmconstructor@>

@<fbmgauss@>

@<fbmsubdivision@>

return FBMCurve

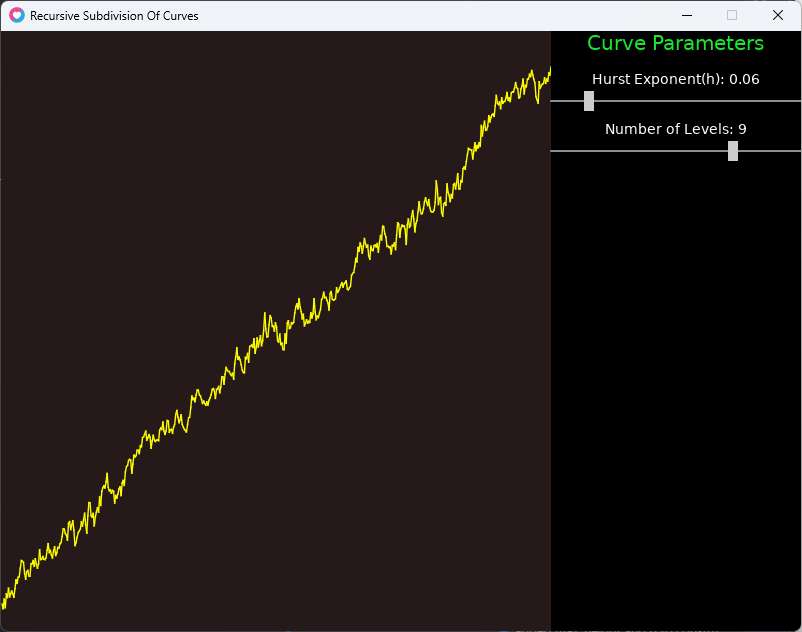
Displaying the Curve

In the final simulation we will see the curve drawn next to a bunch of slider controls which allow us to tweak some of the parameters.
To this end, I will use the ne0luv library (described elsewhere on my website) which contains some utility UI classes.
We will create a new panel called CurvePanel whose only task it to create a new instance of the FBMCurve and display it.
I will not describe this in detail as the code below is self-explanatory.

file: curvepanel.lua

local Class = require('middleclass')
local nl = require('ne0luv')
local FBMCurve = require"fbmcurve"

local CurvePanel = Class('CurvePanel', nl.Panel)

function CurvePanel:initialize(bounds)
    -- call the parent class constructor
    nl.Panel.initialize(self, bounds)

    self.curve = FBMCurve(1, 9, self:getHeight())
end

function CurvePanel:_draw()
    -- draw a warm gray background
    love.graphics.setColor(0.15, 0.1, 0.1)
    love.graphics.rectangle('fill', 0, 0, self:getWidth(), self:getHeight())

    -- draw the curve in yellow
    love.graphics.setColor(1.0, 1.0, 0.0)

    -- delta is window width divided number of points
    local delta = self:getWidth() / self.curve.num_points

    -- draw the curve
    for i = 1, self.curve.num_points - 1 do
        love.graphics.line(i * delta,
            self.curve.points[i], (i + 1) * delta, self.curve.points[i + 1])
    end
end

return CurvePanel

`main.lua`

We bring together the CurvePanel and a couple of slider controls to allow the user to change the values of h and num_levels input parameters.

Again the code is documented below and therefore self-explanatory.

Module Imports & Variables

id: moduleglobal

local nl = require('ne0luv')
local CurvePanel = require"curvepanel"

local layout
local controlLayout
local curvePanel
local hText
local hSlider
local levelText
local levelSlider

`love.load` - Initialization

id: loveload

--- love.load: Called once at the start of the simulation
function love.load()
    -- get the canvas size
    local cw = love.graphics.getWidth()
    local ch = love.graphics.getHeight()

    -- width of the control panel
    local controlPanelWidth = 250

    -- create a layout panel
    layout = nl.Layout(nl.Rect(0, 0, cw, ch), {
        layout = 'row',
    })

    -- create a curve panel
    curvePanel = CurvePanel(nl.Rect(0, 0, cw - controlPanelWidth, ch))

    -- create a control panel
    controlLayout = nl.Layout(nl.Rect(0, 0, controlPanelWidth, ch), {
        layout = 'column',
    })

    -- Hurst Exponent text and slider
    hText = nl.Text(nl.Rect(0, 0, controlPanelWidth, 20), {
        text = "Hurst Exponent(h): " .. curvePanel.curve.h,
        align = 'center',
    })

    hSlider = nl.Slider(nl.Rect(0, 0, controlPanelWidth, 20), {
        minValue = 1,
        maxValue = 500,
        currentValue = curvePanel.curve.h * 1000,
    })

    hSlider:addChangeHandler(function(slider)
        local val = hSlider.currentValue / 1000
        -- round to 2 decimal places
        curvePanel.curve.h = math.floor(val * 100) / 100
        curvePanel.curve:generate()
        hText:setText("Hurst Exponent(h): " .. curvePanel.curve.h)
    end)

    -- Number of levels text and slider
    levelText = nl.Text(nl.Rect(0, 0, controlPanelWidth, 20), {
        text = "Number of Levels: " .. curvePanel.curve.num_levels,
        align = 'center',
    })

    levelSlider = nl.Slider(nl.Rect(0, 0, controlPanelWidth, 20), {
        minValue = 5,
        maxValue = 11,
        currentValue = curvePanel.curve.num_levels,
    })

    levelSlider:addChangeHandler(function(slider)
        curvePanel.curve.num_levels = math.floor(levelSlider.currentValue)
        curvePanel.curve:generate()
        levelText:setText("Number of Levels: " .. curvePanel.curve.num_levels)
    end)

    -- add the curve panel and control panel to the layout
    layout:addChild(curvePanel)

    -- add a text panel saying "FBM Curve Parameter"
    controlLayout:addChild(nl.Text(nl.Rect(0, 0, controlPanelWidth, 30), {
        font = love.graphics.newFont(20),
        text = "Curve Parameters",
        fgColor = {0.1, 0.9, 0.2},
        align = 'center',
    }))

    -- add some empty space at the top with an empty panel
    controlLayout:addChild(nl.Panel(nl.Rect(0, 0, controlPanelWidth, 10)))
    controlLayout:addChild(hText)
    controlLayout:addChild(hSlider)

    -- add some empty space at the top with an empty panel
    controlLayout:addChild(nl.Panel(nl.Rect(0, 0, controlPanelWidth, 10)))
    controlLayout:addChild(levelText)
    controlLayout:addChild(levelSlider)

    layout:addChild(controlLayout)
end

`love.update` - Update the Simulation

id: loveupdate

--- love.update: Called every frame, updates the simulation
function love.update(dt)
    layout:update(dt)
end

`love.draw` - Draw the Simulation

id: lovedraw

--- love.draw: Called every frame, draws the simulation
function love.draw()
    layout:draw()
end

Handle Keyboard/Mouse Events

id: lovekeypressed

-- escape to exit
function love.keypressed(key)
    if key == "escape" then
        love.event.quit()
    end
end

function love.mousepressed(x, y, button)
    layout:mousepressed(x, y, button)
end

function love.mousereleased(x, y, button)
    layout:mousereleased(x, y, button)
end

function love.mousemoved(x, y, dx, dy)
    layout:mousemoved(x, y, dx, dy)
end

file: main.lua

--- main.lua: <Empty> Simulation in LÖVE
-- date: 4/3/2024
-- author: Abhishek Mishra

@<moduleglobal@>

@<loveload@>

@<loveupdate@>

@<lovedraw@>

@<lovekeypressed@>

`conf.lua`

file: conf.lua

--- conf.lua: Config for the love2d game.
--
-- date: 4/3/2024
-- author: Abhishek Mishra

-- canvas size
local canvasWidth = 800
local canvasHeight = 600

function love.conf(t)
    -- set the window title
    t.window.title = "Recursive Subdivision Of Curves"

    -- set the window size
    t.window.width = canvasWidth
    t.window.height = canvasHeight

    -- disable unused modules for performance
    t.modules.joystick = false
    t.modules.physics = false
    t.modules.touch = false

    -- enable console
    -- TODO: turning on console crashes Love2D on Windows,
    -- so it's disabled for now
    -- t.console = true
end

https://neolateral.in/litpd-literate-programming-for-pandoc-markdown ↩
https://doi.org/10.1145/358523.358553 "Alain Fournier, Don Fussell, and Loren Carpenter. 1982. Computer rendering of stochastic models. Commun. ACM 25, 6 (June 1982), 371--384." ↩
https://doi.org/10.1145/358523.358553 "Alain Fournier, Don Fussell, and Loren Carpenter. 1982. Computer rendering of stochastic models. Commun. ACM 25, 6 (June 1982), 371--384." ↩